Seasonal patterns of continuous variable
"...it's the time of the season, when love runs high..."
Seasonal adjustment
Life follows a cyclical pattern for many things: circadian rhythms, daily/weekly habits, weather, climate, etc. We tend to wake up in the morning, perform activities throughout the day, and then sleep at night. We might be more active in the summer, when it's sunny and warm outside, and less active in the winter, when it's cold and we just want to stay inside and bundle up. One can already imagine that if I performed a study where I examined daily activity between two exercise programs, and measured one in the winter and the other in the summer, that I might detect a difference that had nothing to do with the exercise programs themselves. Fortunately for many studies, the randomness of data collection prevents confounding or bias that might occur due to cyclical; however, there are certainly situations in which a failure to adjust for a cyclical effect can result in detecting an association that is not actually real, and merely a result of undetected seasonal effects. We will evaluate some of these situations below.
In time series analysis, there are well-defined methods for adjusting for seasonality, for example, using a model called a 'seasonal ARIMA' model, which includes terms for effects occurring over a longer period of time in addition to those for the period immediately preceding. There are methods that model data as sine/cosine curves and model frequencies of wave oscillations in data trends (called frequency domain approaches), for which we can test for patterns in the data at known/expected frequencies, or search for perhaps unknown or unexpected frequencies. In the next 2-3 posts, we'll dive in and examine these, and other, approaches in detail. As a start, let's examine what happens when we fail to account for cyclical/seasonal effects on the data.
WHAT HAPPENS IF WE IGNORE SEASONALITY
Let's start out with a couple of problems that can result if we fail to account for seasonal effects in out data.
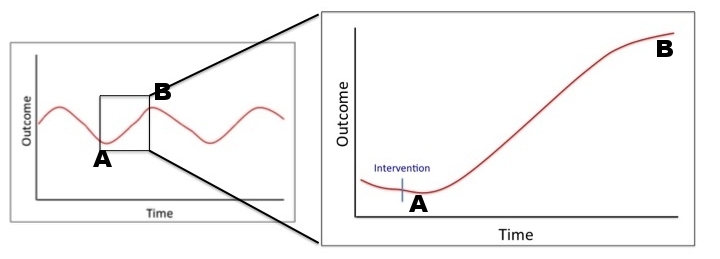
The simplest mistake we can make is to simply ignore, or to not be aware of, a cyclical pattern in our outcome of interest, and to then measure that outcome at two points occurring at difference phases in the cycle. This mistake is demonstrated graphically in Figure 1, which shows a hypothetical outcome that displays an underlying cyclical pattern over time. Let's pretend for a minute that the outcome of interest here is a biomarker level, which as is evident in the full graph on the left, displays a clear cyclical pattern. Now let's say that in a hypothetical experiment, we perform an intervention at time A, and then measure the follow-up at time B. If we were unaware of the cyclical nature of our biomarker (which is not uncommon at all since most novel biomarkers are rarely tracked longitudinally for more than a couple of time points, and thus any cyclical pattern is unknown), then we might come to the erroneous conclusion that our intervention caused the biomarker level to increase (compare average at time A and time B). This example seems trivial, and as discussed above, many biomarker studies overcome the potential cyclical nature through random blood collection (not necessarily by design). However, like many aspects of healthcare, unless we're looking for it, we'll often miss it, and I would postulate that at least one of the reasons for the failure of so many promising biomarkers to make it to prime time has been a lack of appreciation for the need to have a full understanding of their cyclical nature (We'll discuss below some of the methods that can be used to examine these effects).
Figure 1. Hypothetical outcome with a cyclical pattern over time. Outlay shows the mistake of sampling without accounting for the seasonal pattern and incorrectly inferring a positive effect of an intervention.
Another mistake that can occur with failure to account for seasonal changes is shown in Figure 2. We can think of this as the 'rising tide lifts all boats' phenomenon, in which the seasonal effects are such a strong confounder that two otherwise unrelated variables that follow the same seasonal pattern can be perceived to be correlated, even if there is no reason for the two to be correlated. A leaf and a twig floating on the surface of a pond will rise and fall together with waves in the pond, giving someone watching from the side the appearance that the two are correlated; yet, if I reach into the pond and pull out the twig, I would not expect the leaf to come trailing out with it. In the same way, two events that are completely unrelated can appear to be correlated if the two are following the same cyclical pattern. If we do not first adjust for the cyclical pattern in each, we will be unable to appreciate the lack of correlation between the two.
Figure 2. Hypothetical outcomes measured over time. Both outcomes (blue and red lines) appear to be highly correlated due to cyclical nature of each. However, after 'adjusting' for the cyclical nature (inset), we see that there is no clear correlation between the two.
Because the underlying cyclical nature of the outcome is displayed in graphs, the mistakes demonstrated in Figure 1 and 2 seem almost trivial in nature; and, while certainly there are examples from the medical literature in which investigators clearly fail to account for obvious seasonal effects in drawing conclusions, it is not always as easy as this might seem. For example, imagine if all we had from Figure 1 was the inset showing the large effect of the intervention between points A and B. How would be know how to check for seasonality? If Figure 2, if we did not 'zoom in' on the specific values of the red and blue lines at each point after adjusting for the cyclical nature of both, then how would be know that the 'correlation' we measured was only due to shared seasonality? Should we a priori examine our data for seasonality before performing any kind of attempt to correlate variables or assess the effect of an intervention? In the sections (and posts) to follow, we'll start to address some of these questions.
Supervised or unsupervised?
In our prior post examining the correlation between two continuous variables, we performed a periodogram of our activity data and identified the frequency at which there was a dominant peak. The figure below displays that figure again as well as one for daily steps; the code to create this figure is on the related Github page.
Figure 3. Periodograms for Steps and Sleep. Lines denote common frequencies/periods.
This analysis brings up an important question relevant not only to seasonal analysis, but to development of a systematic approach to analysis of monitor data in general:
Is it better to let the data tell us what patterns are present, or should we only ask the data about patterns that are relevant to us?
This question, which relates to the broader idea of supervised vs unsupervised analysis, is particularly important in our examination of seasonal patterns. As shown in Figure 3 for Sleep, the dominant spectral frequency based on the analysis lies at a period of 2.16 days. What exactly is the relevance of 2.16 days? Can we possibly develop a hypothesis about some lifestyle pattern that is occurring every 2.16 days (or 2 days, 3 hours, 50.4 minutes)? (Note: in later posts we'll examine the effect of changing the filtering of the periodogram, which potentially can get rid of some of these uncertain peaks, although there is my no means a fail-proof filtering method that can be applied automatically either). On the other hand, most people have at least a weekly pattern to their activities (frequency ~0.143), and we can see in Figure 3 that there is indeed a spike at this frequency, albeit smaller than at a frequency of 0.46, which corresponds to 2.16 days. Other seasonal periods that could make sense include biweekly (frequency = 0.071) and monthly (frequency = 0.033), although as shown in Figure 3 there is clearly no evidence of a spike at these frequencies.
If we wanted to develop a systematic approach to identifying the seasonal patterns to our data, there are two methods. In method 1, the unsupervised approach, we would let the data tell us the dominant frequency (in this case, 0.46 -> 2.16 days), and develop a method in which we select the frequency based on the highest amplitude of our periodogram. In method 2, the supervised approach, we would select a set of frequencies based on practical possible cycles, and examine each of these against each other (and the null). For example, we could focus our analysis to compare effects of weekly, biweekly, monthly, quarterly, yearly, etc., cycles for the data, and see if inclusion of an interaction term (or other methods discussed in later post) is significant.
Obviously, there is no correct answer to the question of supervised or unsupervised analysis, and it is likely that there will be some circumstances in which we prefer one, and some where we prefer the other. For example, if we're conducting an analysis of Fitbit data where we want to know whether two continuous variables are correlated after adjustment for seasonality (for example, in our analysis of sleep and steps from the prior post), then we might prefer to use the unsupervised approach since it allows us to most fully adjust for the effects of seasonal variation. In that example, seasonality is a nuisance parameter, which means we don't care whether it's 2.16, 4.32, or 21.3; all we care is that it's accounted for in our analysis. In contrast, if I'm analyzing my own data to see if there are any cyclical/seasonal patterns to my daily steps, then it matters what period I use since 7 makes sense as a weekly pattern, but 2.16 doesn't.
In Figure 4, we see another method for supervised analysis for seasonality, in which we examine the average value according to each unit of the cycle (in this case, a period of 7 or 14 days), and then use a simple ANOVA to see whether there was a statistical difference in mean between days. This method provides a nice way both to test and visualize potential seasonality in our data.
Figure 4. Supervised graphs of average numbers of steps and minutes asleep for each day of a weekly and biweekly cycle.
As shown in Figure 4, there is evidence for a seasonal pattern of 1 or 2 weeks for sleep data, but not steps. We can also examine this iteratively using our auto.arima function mentioned in previous posts. The code for these for R is given on our Github page. The results are summarized below:
Sleep:
Weekly cycle: ARIMA(2,0,0)(1,0,0), AIC = 2414.32, log likelihood = -1202.16
Biweekly cycle: ARIMA(0,0,0)(1,0,0), AIC = 2410.64, log likelihood = -1202.32
Steps:
Weekly cycle: ARIMA(0,0,0)(2,0,0), AIC = 4065.03, log likelihood = -2028.52
Biweekly cycle: ARIMA(0,0,0)(1,0,0), AIC = 4063.74, log likelihood = -2028.87
Here we see that broadly an automated approach using the auto.arima function corresponds to the 'manual' ANOVA approach above in that both approaches identified a seasonal pattern for sleep but not steps. Of course, depending on which criteria we used to compare, they may or may not agree within the cycles (most likely this is complicated by the different models identified with the two cycles in which for the weekly cycle two additional autoregressive terms were included...), but it appears that either approach would be reasonable for identification of the underlying seasonal frequency.
At this point I should mention that with regard to my own schedule from which this Fitbit data was collected, I followed a very consistent weekly and biweekly pattern during the period that I was wearing the Fitbit. I almost always engaged in aerobic exercise on Monday, Wednesday, Friday, and almost always slept in on Saturdays and Sundays. I was working two separate positions during the period, alternating between the two each week (hence, the biweekly pattern). For one week, I generally performed desk work (doing statistical analyses like these...) and on the alternate week I was running around doing clinical work in the hospital. Knowing this information ahead of time, I would suggest that any analysis of my sleep or activity data that failed to capture this pattern would be flawed or insensitive. Ultimately, this is a key question to think about going forward. To what degree should we include 'outside' information in conduct of our analyses? This question is the crux of the issue regarding supervised and unsupervised analysis, and one to which we will return often in the future.
Time vs Frequency Domains
No discussion of time series analysis would be complete without a brief mention of the two broad approaches that can be used based on whether we analyze the data in a time or a frequency domain. The simplest way to tell the difference between the two approaches is to check the X-axis for a graph of the data. In time domain analysis, the X-axis is time, as is the case for ARIMA models, and graphs as shown in figure 1 and 2 above. In frequency domain analysis, the X-axis is frequency, as is the case for the periodogram displayed in Figure 3 above. One uses a process called a transformation to convert data between the two domains, with the most commonly used method being called the fast Fournier transform.
Although both approaches can be used to analyze the same data, they do tend to have their strengths and weaknesses. For example, time domain approaches are probably more intuitive to interpret and apply in forecasting data. It is easy to explain that the value of an outcome today is a function of the value yesterday or last week. Frequency approaches tend to require somewhat more thought, particularly for those without formal training in engineering, and because they are based in complex number theory and trigonometric identities (i.e., sine and cosine), they also require more comfort with advanced mathematical concepts. Nonetheless, there are certain assumptions that we must make in the time domain that are unnecessary in the frequency domain. For example, multivariate analysis is much more straightforward in the frequency domain since all variables can be easily analyzed as random variables. In application of time domain approaches, we generally have to resort to the standard regression problem of needing to assign one variable as the fixed regressor (X) and the other as the random (Y) even if both are technically random, resulting in problems such as regression dilution. In the posts to follow, we will explore both approaches in greater depth.
In the next few posts, we'll take a deep dive into approaches to analysis of seasonal patterns in our data. The themes and questions raised in this post will come up often, and hopefully by the end we'll have developed a solid framework for our analyses.